早教吧作业答案频道 -->数学-->
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使
题目详情
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
高二学生日均使用手机时间的频数分布表
(Ⅰ)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
附:随机变量k2=
(其中n=a+b+c+d为样本总量).
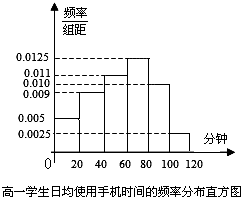 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
高二学生日均使用手机时间的频数分布表
(Ⅰ)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
附:随机变量k2=
(其中n=a+b+c+d为样本总量).

时间分组 频数 [0,20) 12 [20,40) 20 [40,60) 24 [60,80) 26 [80,100) 14 [100,120] 4 时间分组 频数 时间分组 频数 [0,20) 12 [0,20) 12 [20,40) 20 [20,40) 20 [40,60) 24 [40,60) 24 [60,80) 26 [60,80) 26 [80,100) 14 [80,100) 14 [100,120] 4 [100,120] 4
非手机迷 手机迷 合计 男 ___ ___ ___ 女 ___ ___ ___ 合计 ___ ___ ___ 非手机迷 手机迷 合计 非手机迷 手机迷 合计 男 ___ ___ ___ 男 ___ ___ ___ 女 ___ ___ ___ 女 ___ ___ ___ 合计 ___ ___ ___ 合计 ___ ___ ___ k2=
(其中n=a+b+c+d为样本总量).
 k2=
k2=
(其中n=a+b+c+d为样本总量).
 k2=
k2=
(其中n=a+b+c+d为样本总量).
 2=
2=
(其中n=a+b+c+d为样本总量).

n(ad-bc)2 (a+b)(c+d)(a+c)(b+d) n(ad-bc)2 n(ad-bc)2 (ad-bc)2(ad-bc)22 (a+b)(c+d)(a+c)(b+d) (a+b)(c+d)(a+c)(b+d)
参考数据 P(k2≥x0) 0.15 0.10 0.05 0.025 x0 2.072 2.706 3.841 5.024 参考数据 P(k2≥x0) 0.15 0.10 0.05 0.025 参考数据 P(k2≥x0) 200.15 0.10 0.05 0.025 x0 2.072 2.706 3.841 5.024 x0 02.072 2.706 3.841 5.024

高二学生日均使用手机时间的频数分布表
| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
| 非手机迷 | 手机迷 | 合计 | |
| 男 | ___ | ___ | ___ |
| 女 | ___ | ___ | ___ |
| 合计 | ___ | ___ | ___ |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.高二学生日均使用手机时间的频数分布表
| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
| 非手机迷 | 手机迷 | 合计 | |
| 男 | ___ | ___ | ___ |
| 女 | ___ | ___ | ___ |
| 合计 | ___ | ___ | ___ |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |

| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
| 非手机迷 | 手机迷 | 合计 | |
| 男 | ___ | ___ | ___ |
| 女 | ___ | ___ | ___ |
| 合计 | ___ | ___ | ___ |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
 k2=
k2= | n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
 k2=
k2= | n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
 2=
2= | n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |

| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |

▼优质解答
答案和解析
(Ⅰ)由频率分布直方图可知,高一学生是“手机迷”的概率为P11=(0.0025+0.010)×20=0.25(2分)
由频数分布表可知,高二学生是“手机迷”的概率为P2=
=0.18(4分)
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
(8分)
将2×2列联表中的数据代入公式计算,得k2=
=
=
≈3.030(11分)
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) P2=
=0.18(4分)
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
(8分)
将2×2列联表中的数据代入公式计算,得k2=
=
=
≈3.030(11分)
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) 2=
14+4 100 14+4 14+4 14+4100 100 100=0.18(4分)
因为P11>P22,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
非手机迷 手机迷 合计 男 30 15 45 女 45 10 55 合计 75 25 100 非手机迷 手机迷 合计 非手机迷 非手机迷手机迷 手机迷合计 合计男 30 15 45 男 男30 3015 1545 45 女 45 10 55 女 女45 4510 1055 55合计 75 25 100 合计 合计75 7525 25100 100(8分)
将2×2列联表中的数据代入公式计算,得k2=
=
=
≈3.030(11分)
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) k2=
=
=
≈3.030(11分)
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) 2=
n(ad-bc)2 (a+b)(c+d)(a+c)(b+d) n(ad-bc)2 n(ad-bc)2 n(ad-bc)22(a+b)(c+d)(a+c)(b+d) (a+b)(c+d)(a+c)(b+d) (a+b)(c+d)(a+c)(b+d)=
100×(30×10-45×15)2 75×25×45×55 100×(30×10-45×15)2 100×(30×10-45×15)2 100×(30×10-45×15)2275×25×45×55 75×25×45×55 75×25×45×55=
100 33 100 100 10033 33 33≈3.030(11分)
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分)
由频数分布表可知,高二学生是“手机迷”的概率为P2=
| 14+4 |
| 100 |
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,得k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100×(30×10-45×15)2 |
| 75×25×45×55 |
| 100 |
| 33 |
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) P2=
| 14+4 |
| 100 |
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,得k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100×(30×10-45×15)2 |
| 75×25×45×55 |
| 100 |
| 33 |
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) 2=
| 14+4 |
| 100 |
因为P11>P22,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,得k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100×(30×10-45×15)2 |
| 75×25×45×55 |
| 100 |
| 33 |
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100×(30×10-45×15)2 |
| 75×25×45×55 |
| 100 |
| 33 |
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分) 2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100×(30×10-45×15)2 |
| 75×25×45×55 |
| 100 |
| 33 |
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分)
看了 某学校为了了解学生使用手机的...的网友还看了以下:
一个工厂有两个生产车间,甲车间人数占两个车间总人数的百分之六十:如果从加车间调24人去乙车间,乙车 2020-04-09 …
已知动点M与两个O(0,0),A(3,0)的距离之比为1:2,点M的轨迹曲线为C,求曲线C的方程要 2020-05-15 …
(2014•天津)图a、b分别为农村和城市生态系统的生物量(生命物质总量)金字塔示意图.下列叙述正 2020-06-13 …
三个生成组共同负责建造7个蔬菜大棚,甲实际建4个大棚,乙实际建3个大棚,丙一个未建,建好后丙付给甲 2020-06-16 …
谁能帮我把这段话透彻的理解一下.n个命题变项共产生p=2^n个不同的赋值,而任何公式在每种赋值情况 2020-06-18 …
有位同学制作了两个生态模拟系统装置瓶,第一个里面有瓶塞,池水,金鱼藻,椎实螺和池泥.第二个里面有瓶 2020-06-21 …
研究人员在对甲、乙两个不同的生态系统调查后发现,两个生态系统的生产者总能量相同,甲生态系统只有初级 2020-06-22 …
编写一个程序,计算两个非0实数的加、减、乘、除运算的结果(要求输入两个非0实数,输出运算结果) 2020-06-27 …
急,编写一个程序,计算两个非0实数的加、减、乘、除运算的结果.(要求输入两个非0实数,输出运算结果 2020-06-27 …
一道数学应用题`挺有意思的`就是没整懂`高手来``在设计数字电子计算机中,必须考虑选用什么样的数制 2020-07-11 …