早教吧作业答案频道 -->数学-->
如图，直线OA：y=12x的图象与反比例函数y=kx（k≠0）在第一象限的图象交于A点，过A点作轴的垂线，垂足为M，已知△OAM的面积为1．（1）求反比例函数的解析式；（2）如果B为反比例函数在第
题目详情
如图，直线OA：y=
x的图象与反比例函数y=
（k≠0）在第一象限的图象交于A点，过A点作轴的垂线，垂足为M，已知△OAM的面积为1．
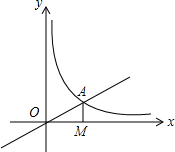
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．如图，直线OA：y=
x的图象与反比例函数y=
（k≠0）在第一象限的图象交于A点，过A点作轴的垂线，垂足为M，已知△OAM的面积为1．
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
x的图象与反比例函数y=
（k≠0）在第一象限的图象交于A点，过A点作轴的垂线，垂足为M，已知△OAM的面积为1．
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
1 2 1 1 2 2
（k≠0）在第一象限的图象交于A点，过A点作轴的垂线，垂足为M，已知△OAM的面积为1．
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
k x k k x x
| 1 |
| 2 |
| k |
| x |
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．如图，直线OA：y=
| 1 |
| 2 |
| k |
| x |
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
| 1 |
| 2 |
| k |
| x |
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
| 1 |
| 2 |
| k |
| x |
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
| k |
| x |
▼优质解答
答案和解析
（1）设点A的坐标为（a，b），
则
，解得：k=2．
∴反比例函数的解析式为y=
．
（2）联立直线OA和反比例函数解析式得：
，解得：
．
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
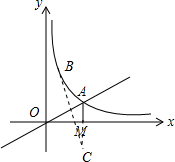
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
，解得：
．
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
b=
ab=1b=
b=
b=
k a k k ka a a
ab=1
ab=1
1 2 1 1 12 2 2ab=1
∴反比例函数的解析式为y=
．
（2）联立直线OA和反比例函数解析式得：
，解得：
．
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
，解得：
．
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
2 x 2 2 2x x x．
（2）联立直线OA和反比例函数解析式得：
，解得：
．
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
，解得：
．
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
y=
y=
x y=
y=
y=
2 x 2 2 2x x xy=
x y=
x y=
1 2 1 1 12 2 2x
．
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
，解得：
．
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
x=2 y=1 x=2 x=2 x=2y=1 y=1 y=1
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
，解得：
．
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
2=m+n -1=2m+n 2=m+n 2=m+n 2=m+n-1=2m+n -1=2m+n -1=2m+n
．
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
m=-3 n=5 m=-3 m=-3 m=-3n=5 n=5 n=5
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
．
∴P点的坐标为（
5 3 5 5 53 3 3．
∴P点的坐标为（
举报
问题解析 问题解析
（1）设点A的坐标为（a，b），由点A在反比例函数图象上结合三角形△OAM的面积为1，可得出关于k、a、b的三元一次方程组，解方程即可求出k值，从而得出反比例函数解析式；
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标． （1）设点A的坐标为（a，b），由点A在反比例函数图象上结合三角形△OAM的面积为1，可得出关于k、a、b的三元一次方程组，解方程即可求出k值，从而得出反比例函数解析式；
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．名师点评 名师点评
本题考点： 本题考点：
反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
考点点评： 考点点评：
本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键． 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
扫描下载二维码
扫描下载二维码
©2020 作业帮 联系方式：service@zuoyebang.com
作业帮协议作业帮协议
var userCity = "\u4e50\u5c71",
userProvince = "\u56db\u5ddd",
zuowenSmall = "3";
则
|
∴反比例函数的解析式为y=
| 2 |
| x |
（2）联立直线OA和反比例函数解析式得：
|
|
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
|
|
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
|
b=
| ||
|
b=
| ||
|
b=
| ||
|
b=
| ||
|
| k |
| a |
| 1 |
| 2 |
| k |
| a |
| k |
| a |
| k |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴反比例函数的解析式为y=
| 2 |
| x |
（2）联立直线OA和反比例函数解析式得：
|
|
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
|
|
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
| 2 |
| x |
（2）联立直线OA和反比例函数解析式得：
|
|
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
|
|
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
|
y=
| ||
y=
|
y=
| ||
y=
|
y=
| ||
y=
|
y=
| ||
y=
|
| 2 |
| x |
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
|
|
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
|
| x=2 |
| y=1 |
| x=2 |
| y=1 |
| x=2 |
| y=1 |
| x=2 |
| y=1 |
∴点A的坐标为（2，1）．
设A点关于x轴的对称点为C，则C点的坐标为（2，-1），连接BC较x轴于点P，点P即为所求．如图所示．
设直线BC的解析式为y=mx+n，
由题意可得：B点的坐标为（1，2），
∴
|
|
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
|
| 2=m+n |
| -1=2m+n |
| 2=m+n |
| -1=2m+n |
| 2=m+n |
| -1=2m+n |
| 2=m+n |
| -1=2m+n |
|
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
|
| m=-3 |
| n=5 |
| m=-3 |
| n=5 |
| m=-3 |
| n=5 |
| m=-3 |
| n=5 |
∴BC的解析式为y=-3x+5．
当y=0时，0=-3x+5，解得：x=
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
| 5 |
| 3 |
∴P点的坐标为（
|
作业帮用户
2017-01-20
举报
|
|
作业帮用户
2017-01-20
举报
|
作业帮用户
2017-01-20
举报
- 问题解析
- （1）设点A的坐标为（a，b），由点A在反比例函数图象上结合三角形△OAM的面积为1，可得出关于k、a、b的三元一次方程组，解方程即可求出k值，从而得出反比例函数解析式；
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．
- 名师点评
-
- 本题考点：
- 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
-
- 考点点评：
- 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
作业帮用户
2017-01-20
举报
- 问题解析
- （1）设点A的坐标为（a，b），由点A在反比例函数图象上结合三角形△OAM的面积为1，可得出关于k、a、b的三元一次方程组，解方程即可求出k值，从而得出反比例函数解析式；
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．
- 名师点评
-
- 本题考点：
- 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
-
- 考点点评：
- 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
作业帮用户
2017-01-20
举报
- 问题解析
- （1）设点A的坐标为（a，b），由点A在反比例函数图象上结合三角形△OAM的面积为1，可得出关于k、a、b的三元一次方程组，解方程即可求出k值，从而得出反比例函数解析式；
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．
- 名师点评
-
- 本题考点：
- 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
-
- 考点点评：
- 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
作业帮用户
2017-01-20
举报
作业帮用户作业帮用户
2017-01-202017-01-20
举报
举报
- 问题解析
- （1）设点A的坐标为（a，b），由点A在反比例函数图象上结合三角形△OAM的面积为1，可得出关于k、a、b的三元一次方程组，解方程即可求出k值，从而得出反比例函数解析式；
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．
（2）联立直线与反比例函数解析式求出点A的坐标，找出点A关于x轴的对称点C的坐标，再结合反比例函数解析式求出点B坐标，连接BC即可找出点P的位置，由点B、C的坐标利用待定系数法即可求出直线BC的解析式，令y=0求出x值即可得出点P的坐标．
- 名师点评
-
- 本题考点：
- 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
-
- 考点点评：
- 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
- 本题考点：
- 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
- 本题考点：
- 反比例函数与一次函数的交点问题 反比例函数图象上点的坐标特征 轴对称-最短路线问题
- 考点点评：
- 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
- 考点点评：
- 本题考查了直线与反比例函数图象的交点问题、轴对称中的最短线路问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及解多元一次方程组，解题的关键是：（1）得出关于k、a、b的三元一次方程组；（2）确定点P的位置．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标，利用待定系数法求出函数解析式是关键．
扫描下载二维码
扫描下载二维码
©2020 作业帮 联系方式：service@zuoyebang.com
作业帮协议作业帮协议
var userCity = "\u4e50\u5c71",
userProvince = "\u56db\u5ddd",
zuowenSmall = "3";
看了 如图，直线OA：y=12x的...的网友还看了以下：
1.PT切圆O于T,CT为直径,D为OC上的一点,支线PD交圆O于B和A,B在线段PD上,若CD= 2020-04-12 …
初二数学题含有一个未知数,并且未知数的最高次指数是2的方程,叫做一元二次方程.如：x2-2x+l= 2020-07-10 …
如图,已知AB是圆O的直径,直线l与圆O相切于点C,且弧AC=弧AD,CD交AB于E,BF⊥l,垂 2020-07-31 …
已知：如图，点P是半径为5cm的⊙O外的一点，OP=13cm，PT切⊙O于T，过P点作⊙O的割线P 2020-07-31 …
已知：如图，点P是半径为5cm的⊙O外的一点，OP=13cm，PT切⊙O于T，过P点作⊙O的割线P 2020-07-31 …
已知关于x的不等式组5-2x≥-1x-a大于0无解,a的取值范围是≥3若只将不等式组中X-a>o改 2020-07-31 …
已知直线圆EM经过圆O的圆心,分别交圆O于B,C两点,直线EM与圆O相切于点A,CD垂直EM于点D 2020-07-31 …
已知:AB为⊙O的直径,C是⊙O外一点,BC交⊙O于点E,AC交⊙O于点D,∠DOE=60º.求∠C 2020-11-27 …
已知：如图，点P是半径为5cm的⊙O外的一点，OP=13cm，PT切⊙O于T，过P点作⊙O的割线PA 2020-12-05 …
求2009年的济南的中考数学题：已知AB是圆O的直径,CA与圆O相切于点A,连接CO交圆O于点D,C 2021-01-22 …