关于人体的脂肪含量(百分比)和年龄关系的研究中得到如下一组数据:年龄102327394145495053脂肪8.79.517.821.227.526.328.229.631.8

Question

关于人体的脂肪含量(百分比)和年龄关系的研究中 得到如下一组数据:

年龄	10	23	27	39	41	45	49	50	53
脂肪	8.7	9.5	17.8	21.2	27.5	26.3	28.2	29.6	31.8

    判断它们是否有相关关系 若有 作一拟合直线.

关于人体的脂肪含量(百分比)和年龄关系的研究中 得到如下一组数据:

年龄	10	23	27	39	41	45	49	50	53
脂肪	8.7	9.5	17.8	21.2	27.5	26.3	28.2	29.6	31.8

    判断它们是否有相关关系 若有 作一拟合直线.

年龄	10	23	27	39	41	45	49	50	53
脂肪	8.7	9.5	17.8	21.2	27.5	26.3	28.2	29.6	31.8

年龄

10

23

27

39

41

45

49

50

53

脂肪

8.7

9.5

17.8

21.2

27.5

26.3

28.2

29.6

31.8

年龄

10

23

27

39

41

45

49

50

53

年龄

年龄

10

10

23

23

27

27

39

39

41

41

45

45

49

49

50

50

53

53

脂肪

8.7

9.5

17.8

21.2

27.5

26.3

28.2

29.6

31.8

脂肪

脂肪

8.7

8.7

9.5

9.5

17.8

17.8

21.2

21.2

27.5

27.5

26.3

26.3

28.2

28.2

29.6

29.6

31.8

31.8

    判断它们是否有相关关系 若有 作一拟合直线.

Answer 1

思路分析： 涉及两个变量:年龄与脂肪含量 可以年龄为自变量 考察脂肪含量的变化趋势 而分析相关关系 通常借助散点图.

解 : 以年龄作为x轴 y轴表示脂肪含量 可得相应散点图

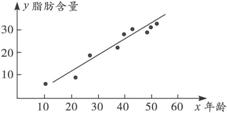
由上图知 两者具有相关关系.

思路分析： 涉及两个变量:年龄与脂肪含量 可以年龄为自变量 考察脂肪含量的变化趋势 而分析相关关系 通常借助散点图.

思路分析： 思路分析： 涉及两个变量:年龄与脂肪含量 可以年龄为自变量 考察脂肪含量的变化趋势 而分析相关关系 通常借助散点图.

解 : 以年龄作为x轴 y轴表示脂肪含量 可得相应散点图

解 解 : : 以年龄作为x轴 y轴表示脂肪含量 可得相应散点图

由上图知 两者具有相关关系.

由上图知 两者具有相关关系.