早教吧作业答案频道 -->数学-->
如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.①依题意,请在图2中补全图形;②如果BP
题目详情
如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.
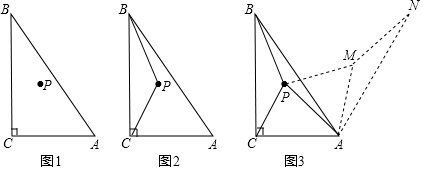
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长.
(2)如图3,连接PA,PB,PC,求PA+PB+PC的最小值.
小慧的作法是:以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,那么就将PA+PB+PC的值转化为CP+PM+MN的值,连接CN,当点P落在CN上时,此题可解.
请你参考小慧的思路,在图3中证明PA+PB+PC=CP+PM+MN.
并直接写出当AC=BC=4时,PA+PB+PC的最小值.如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.

(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长.
(2)如图3,连接PA,PB,PC,求PA+PB+PC的最小值.
小慧的作法是:以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,那么就将PA+PB+PC的值转化为CP+PM+MN的值,连接CN,当点P落在CN上时,此题可解.
请你参考小慧的思路,在图3中证明PA+PB+PC=CP+PM+MN.
并直接写出当AC=BC=4时,PA+PB+PC的最小值.


(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长.
(2)如图3,连接PA,PB,PC,求PA+PB+PC的最小值.
小慧的作法是:以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,那么就将PA+PB+PC的值转化为CP+PM+MN的值,连接CN,当点P落在CN上时,此题可解.
请你参考小慧的思路,在图3中证明PA+PB+PC=CP+PM+MN.
并直接写出当AC=BC=4时,PA+PB+PC的最小值.如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.

(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长.
(2)如图3,连接PA,PB,PC,求PA+PB+PC的最小值.
小慧的作法是:以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,那么就将PA+PB+PC的值转化为CP+PM+MN的值,连接CN,当点P落在CN上时,此题可解.
请你参考小慧的思路,在图3中证明PA+PB+PC=CP+PM+MN.
并直接写出当AC=BC=4时,PA+PB+PC的最小值.

▼优质解答
答案和解析
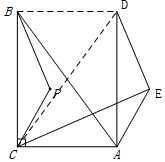
(1)①补全图形如图所示;
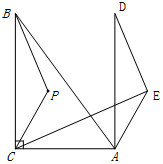
②如图,连接BD、CD
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中,CE=
=
=
=3
;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.
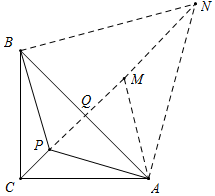
由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
CD2-DE2 CD2-DE2 CD2-DE2 CD2-DE22-DE22=
=
=3
;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
36-9 36-9 36-9 36-9=
=3
;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
27 27 27 27=3
;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
. 3
3 3 3 3;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
2 2 2 2,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
1 2 1 1 12 2 2AB=2
=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
2 2 2 2=CQ,NQ=
AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
3 3 3 3AQ=2
,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
.
6 6 6 6,
∴此时CN=CP+PM+MN=PA+PB+PC=2
+2
. 2
2 2 2 2+2
6 6 6 6.

②如图,连接BD、CD

∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中,CE=
| CD2-DE2 |
| 36-9 |
| 27 |
| 3 |
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
| 2 |
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| CD2-DE2 |
| 36-9 |
| 27 |
| 3 |
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
| 2 |
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 36-9 |
| 27 |
| 3 |
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
| 2 |
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 27 |
| 3 |
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
| 2 |
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 3 |
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.

由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4
| 2 |
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 2 |
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 2 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 3 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 6 |
∴此时CN=CP+PM+MN=PA+PB+PC=2
| 2 |
| 6 |
| 2 |
| 6 |
看了 如图1,在△ABC中,∠AC...的网友还看了以下:
读经纬网示意图,回答第11-14题关于图中各点方向的判断,正确的是()A.b点在a点的东南方向B. 2020-05-13 …
读下面某学校平面示意图,回答1-2题。1、根据图示指向标,判断该学校大门的朝向为[]A.东南方向B 2020-05-13 …
下图为目前世界主要板块接触关系示意图,读图回答1—3题。1、飞机从M地沿最短路径飞往P地,飞行方向 2020-05-13 …
读“沿某一理想大陆45°N所作的剖面示意图”,回答16-17题.若图中M、N表示近地面的等压面,则 2020-05-13 …
时标网络计划中虚工作以( )的虚线表示。 A.水平方向 B.垂直方向 C.任意方向 D.双向 2020-05-18 …
A是n行n列的矩阵,则A是可逆矩阵的充分必要条件是A:A的任意列向量是非零向量B:A的任意行向量是 2020-07-31 …
读地球公转示意图,完成下列题目:(1)请在E处短线上补画箭头,表示地球公转方向.(2)当地球在公转轨 2020-12-05 …
下列结论中,正确的是A.若向量a的方向是任意的,则a=0B.若向量a、b满足a+b=0,则a=b=0 2020-12-07 …
关于善意取得的问题。A的手表弄丢了,被B捡到。在B占有期间C偷走手表。C将表卖至市场。D用市价将手表 2020-12-26 …
如图为某学校平面示意图,据图回答18~19题.根据图示指向标,判断该学校大门的朝向为()A.东南方向 2021-01-15 …