早教吧作业答案频道 -->数学-->
观察发现(1)如图1,四边形ABCD和四边形AEFG都是正方形,且点E在边AB上,连接DE和BG,猜想线段DE与BG的数量关系和位置关系.(只要求写出结论,不必说出理由)深入探究(2)如图
题目详情
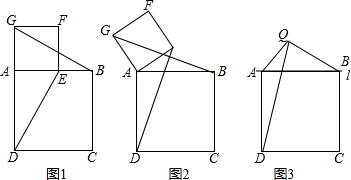
【观察发现】(1)如图1,四边形ABCD和四边形AEFG都是正方形,且点E在边AB上,连接DE和BG,猜想线段DE与BG的数量关系和位置关系.(只要求写出结论,不必说出理由)
【深入探究】(2)如图2,将图1中正方形AEFG绕点A逆时针旋转一定的角度,其他条件与观察发现中的条件相同,观察发现中的结论是否还成立?请根据图2加以说明.
【拓展应用】(3)如图3,直线l上有两个动点A、B,直线l外有一点动点Q,连接QA,QB,以线段AB为边在l的另一侧作正方形ABCD,连接QD.随着动点A、B的移动,线段QD的长也会发生变化,若QA,QB长分别为3
,6保持不变,在变化过程中,线段QD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
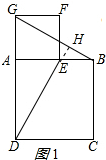
【深入探究】(2)如图2,将图1中正方形AEFG绕点A逆时针旋转一定的角度,其他条件与观察发现中的条件相同,观察发现中的结论是否还成立?请根据图2加以说明.
【拓展应用】(3)如图3,直线l上有两个动点A、B,直线l外有一点动点Q,连接QA,QB,以线段AB为边在l的另一侧作正方形ABCD,连接QD.随着动点A、B的移动,线段QD的长也会发生变化,若QA,QB长分别为3
| 2 |

▼优质解答
答案和解析
(1)  DE=BG,DE⊥BG;理由如下:
DE=BG,DE⊥BG;理由如下:
延长DE交BG于H,如图1所示:
∵四边形ABCD、四边形AEFG都是正方形,
∴AB=AD,AG=AE,∠EAD=∠BAG=90°,
在△BAG与△DAE中,
,
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE,
∵∠AGB+∠ABG=90°,
∴∠AGB+∠ADE=90°,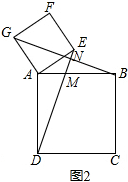
∴∠DHG=90°,
∴DE⊥BG;
(2) (1)中的结论成立,即DE=BG,DE⊥BG;
理由如下:如图2所示,
∵四边形ABCD、四边形AEFG都是正方形,
∴BA=AD,AG=AE,∠BAD=∠EAG=90°,
∴∠BAG+∠BAE=∠EAG+∠BAE,
即∠BAG=∠DAE,在△BAG与△DAE中,
,
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE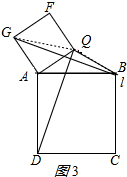
∵∠AMD+∠ADE=90°,∠AMD=∠BME,
∴∠BME+∠ABG=90°,
∴∠DNB=90°,
∴DE⊥BG;
(3) QD存在最大值;理由如下:
以QA为边作正方形QAGF,连接QG、BG,如图3所示:
则QG=
QA=4,
由(2)可得:QD=BG,
当G、Q、B三点共线时,BG最长,
此时BC=QG+QB=4+4=8,
即线段QD长的最大值为8.
 DE=BG,DE⊥BG;理由如下:
DE=BG,DE⊥BG;理由如下:延长DE交BG于H,如图1所示:
∵四边形ABCD、四边形AEFG都是正方形,
∴AB=AD,AG=AE,∠EAD=∠BAG=90°,
在△BAG与△DAE中,
|
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE,
∵∠AGB+∠ABG=90°,
∴∠AGB+∠ADE=90°,

∴∠DHG=90°,
∴DE⊥BG;
(2) (1)中的结论成立,即DE=BG,DE⊥BG;
理由如下:如图2所示,
∵四边形ABCD、四边形AEFG都是正方形,
∴BA=AD,AG=AE,∠BAD=∠EAG=90°,
∴∠BAG+∠BAE=∠EAG+∠BAE,
即∠BAG=∠DAE,在△BAG与△DAE中,
|
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE

∵∠AMD+∠ADE=90°,∠AMD=∠BME,
∴∠BME+∠ABG=90°,
∴∠DNB=90°,
∴DE⊥BG;
(3) QD存在最大值;理由如下:
以QA为边作正方形QAGF,连接QG、BG,如图3所示:
则QG=
| 2 |
由(2)可得:QD=BG,
当G、Q、B三点共线时,BG最长,
此时BC=QG+QB=4+4=8,
即线段QD长的最大值为8.
看了 观察发现(1)如图1,四边形...的网友还看了以下:
已知a、b满足2a+8+|b-3|=0,解关于x的方程(a+2)x+b2=a-1. 2020-06-04 …
简谐振动中弹簧振子所走路程与时间的关系1.一个物体做简谐运动时,周期是T,振幅是A,那么物体()A 2020-06-06 …
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax-1,其中a>0,a≠1.(1)求f( 2020-06-09 …
设f(x)=loga(x-2a)+loga(x-3a),其中a>0且a≠1.(1)已知f(4a)= 2020-06-12 …
选词填空。查阅阅读阅历.联系关系1.今天,我()了中国四大名著之一《西游记》。2.()有关中华姓氏 2020-06-13 …
已知:a、b为实数,关于x的方程x2-(a-1)x+b+3=0的一个实根为a+1.(1)用含a的代 2020-06-22 …
已知函数f(x)=ax2-(2a+1)x+a+1.(1)若a=2,解关于x的不等式f(x)≥0;( 2020-07-16 …
已知a∈R,命题p:实系数一元二次方程x2+ax+2=0的两根都是虚数;命题q:存在复数z同时满足 2020-07-16 …
设A为n阶矩阵.若存在正整数m使Am=O,则称A为n阶幂零矩阵.现设A为n阶幂零矩阵,E为n阶单位 2020-07-22 …
已知a>0且a≠1.命题P:对数loga(-2t2+7t-5)有意义,Q:关于实数t的不等式t2- 2020-07-29 …