早教吧作业答案频道 -->数学-->
如图,以△ABC的各边为边,在BC的同一侧作等边三角形DBC,等边三角形ABE,等边三角形△ACF.(1)求证:四边形AEDF是平行四边形;(2)△ABC满足何条件,四边形AEDF是菱形?请说明理由.
题目详情
如图,以△ABC的各边为边,在BC的同一侧作等边三角形DBC,等边三角形ABE,等边三角形△ACF.
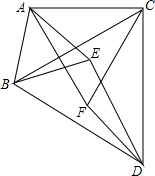
(1)求证:四边形AEDF是平行四边形;
(2)△ABC满足何条件,四边形AEDF是菱形?请说明理由.

(1)求证:四边形AEDF是平行四边形;
(2)△ABC满足何条件,四边形AEDF是菱形?请说明理由.
▼优质解答
答案和解析
(1)证明:∵△ABE和△CBD为等边三角形,
∴∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,
∴∠ABC=∠EBD,
在△ABC和△EBD中
,
∴△ABC≌△EBD,
∴AC=DE,
∵△ACF为等边三角形,
∴AC=CF=AF,
∴AF=DE,
同理可证得△ACB≌△FCD,
∴AB=DF,
而AB=AE,
∴AE=DF,
∴四边形AEDF是平行四边形;
(2) △ABC满足AB=AC时,四边形AEDF是菱形.理由如下:
∵四边形AEDF是平行四边形,
∴当AE=AF时,四边形AEDF是菱形,
此时AB=AC,
∴当AB=AC时,四边形AEDF是菱形.
∴∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,
∴∠ABC=∠EBD,
在△ABC和△EBD中
|
∴△ABC≌△EBD,
∴AC=DE,
∵△ACF为等边三角形,
∴AC=CF=AF,
∴AF=DE,
同理可证得△ACB≌△FCD,
∴AB=DF,
而AB=AE,
∴AE=DF,
∴四边形AEDF是平行四边形;
(2) △ABC满足AB=AC时,四边形AEDF是菱形.理由如下:
∵四边形AEDF是平行四边形,
∴当AE=AF时,四边形AEDF是菱形,
此时AB=AC,
∴当AB=AC时,四边形AEDF是菱形.
看了如图,以△ABC的各边为边,在...的网友还看了以下:
三角形三边为ABC,且ABC满足等式3(A方+B方+C方)=(A+B+C)方,请说明三角形ABC是 2020-05-15 …
小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限 2020-07-03 …
已知四边形ABCD的四边分别有a,b,c,d.其中a,c是对边且a2+b2+c2+d2=2ac+2 2020-07-09 …
四边形没有稳定性,当四边形形状改变时,发生变化的是()A.四边形的边长B.四边形的周长C.四边形内 2020-07-22 …
三角形面积公式设三角形三边分别为a、b、c,内切圆半径为r则三角形面积=(a+b+c)r/2设三角 2020-07-31 …
三角形三边长a、b、c满足(a-b-c)(b-c)=0,则这个三角形是()A.等边三角形B.等腰三 2020-08-02 …
正方形ABCD中,以对角线BD为边作菱形BDFE,使B、C、E三点在同一条直线上,连接BF,交CD于 2020-12-25 …
初二菱形的判定四边形四边依次为a,b,c,d,且满足a平方+b平方+c平方+d平方-ab-bc-cd 2021-01-22 …
一个直角三角形底边长为B高为A斜长为C知道AB求C知道AC求B知道BC求A的公式是什么.同上换成锐角 2021-02-05 …
(1)已知三角形ABC中2B=A+C,且边长b=3,c=2求边长a.(2)ABC面积为16(1)已知 2021-02-07 …