早教吧作业答案频道 -->数学-->
在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.(1)若G,H分别是AB,DC中点,求
题目详情
在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
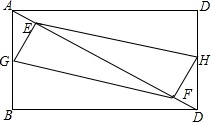
(1)若G,H分别是AB,DC中点,求证:四边形EGFH始终是平行四边形.
(2)在(1)条件下,当t为何值时,四边形EGFH为矩形.
(3)若G,H分别是折线A-B-C,C-D-A上的动点,与E,F相同的速度同时出发,当t为何值时,四边形EGFH为菱形.

(1)若G,H分别是AB,DC中点,求证:四边形EGFH始终是平行四边形.
(2)在(1)条件下,当t为何值时,四边形EGFH为矩形.
(3)若G,H分别是折线A-B-C,C-D-A上的动点,与E,F相同的速度同时出发,当t为何值时,四边形EGFH为菱形.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=
=5,∠GAF=∠HCE,
∵G,H分别是AB,DC中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG和△CEH中,
,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(2) 由(1)得:BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=4,当EF=GH=4时,平行四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5-2t=4,
解得:t=0.5;
②AE=CF=t,EF=5-2(5-t)=4,
解得:t=4.5;
综上所述:当t为0.5s或4.5s时,四边形EGFH为矩形.
(3)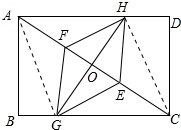 连接AG、CH,如图所示:
连接AG、CH,如图所示:
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH是菱形,
∴AG=CG,
设AG=CG=x,则BG=4-x,
由勾股定理得:AB2+BG2=AG2,
即32+(4-x)2=x2,
解得:x=
,
∴BG=4-
=
,
∴AB+BG=3+
=
,
即t为
s时,四边形EGFH为菱形.
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=
| 32+42 |
∵G,H分别是AB,DC中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG和△CEH中,
|
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(2) 由(1)得:BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=4,当EF=GH=4时,平行四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5-2t=4,
解得:t=0.5;
②AE=CF=t,EF=5-2(5-t)=4,
解得:t=4.5;
综上所述:当t为0.5s或4.5s时,四边形EGFH为矩形.
(3)
 连接AG、CH,如图所示:
连接AG、CH,如图所示:∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH是菱形,
∴AG=CG,
设AG=CG=x,则BG=4-x,
由勾股定理得:AB2+BG2=AG2,
即32+(4-x)2=x2,
解得:x=
| 25 |
| 8 |
∴BG=4-
| 25 |
| 8 |
| 7 |
| 8 |
∴AB+BG=3+
| 7 |
| 8 |
| 31 |
| 8 |
即t为
| 31 |
| 8 |
看了在矩形ABCD中,AB=3,B...的网友还看了以下:
有两个大小形状完全相同的条形磁体A,B(质量也相同) 但A磁性大于B 将它们的异名磁极互相靠近有两 2020-05-14 …
如何用两条直线将一个正方形分成四个相同形状的图形?(要三种分法)请用图形表示 2020-05-16 …
对中国某一位近现代历史人物某一方面的评价,有个相对形成的评价我不需要网上复制黏贴的,我想要的是某一 2020-05-17 …
2个相同形状的物体,各有5个,不重复排列,会有多少可能2个相同形状的物体,各有5个,共十个,要求不 2020-06-11 …
下列条件中不能判断两个三角形一定全等的是()A.两条直角边对应相等的两个直角三角形B.三条边对应相 2020-07-15 …
下列命题中,不正确的是()帮我A.如果两个三角形全等,那么这两个三角形相似.B.如果两个三角形相似 2020-07-30 …
下列图形中,不一定相似的是A邻边之比相等的两个矩形B四条边对应成比例的两个四边形C有一个角相等的两 2020-07-30 …
不正确的是:A.两个三角形相似,且有一条边相等,则两个三角形全等B.两个三角形相似,且周长相等,则 2020-08-01 …
有两个三角形不在同一个平面内,它们的边两两对应平形,那么这两个三角形A:全等,B:相似,C:有一个 2020-08-01 …
三道关于相似多边形的题!一个四边形和一个五变形能相似吗?为什么?两个四边形对应边成比例,三对对应角 2020-08-02 …