早教吧作业答案频道 -->数学-->
如图,长方形OABC的顶点A、C、O都在坐标轴上,点B的坐标为(9,4),E为BC边上一点,CE=6.(1)求点E的坐标和△ABE的周长;(2)若P是OA上的一个动点,它以每秒1个单位长度的速度从点O出
题目详情
如图,长方形OABC的顶点A、C、O都在坐标轴上,点B的坐标为(9,4),E为BC边上一点,CE=6.
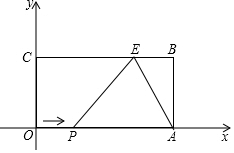
(1)求点E的坐标和△ABE的周长;
(2)若P是OA上的一个动点,它以每秒1个单位长度的速度从点O出发沿射线OA运动,设点P运动的时间为t秒(t>0).
①当t为何值时,△PAE的面积等于△PCE的面积的一半;
②当t为何值时,△PAE为直角三角形.

(1)求点E的坐标和△ABE的周长;
(2)若P是OA上的一个动点,它以每秒1个单位长度的速度从点O出发沿射线OA运动,设点P运动的时间为t秒(t>0).
①当t为何值时,△PAE的面积等于△PCE的面积的一半;
②当t为何值时,△PAE为直角三角形.
▼优质解答
答案和解析
 (1)如图,∵长方形OABC中,点B的坐标为(9,4),
(1)如图,∵长方形OABC中,点B的坐标为(9,4),
∴CB=9,CO=4=AB,
又∵CE=6,
∴E(6,4),BE=3,
∵∠B=90°,
∴Rt△ABE中,AE=
=5,
∴△ABE的周长:3+4+5=12;
(2)①∵OP=1×t=t,
∴AP=9-t,
∵△PAE的面积等于△PCE的面积的一半,
∴当P在OA之间时,
根据
×AP×AB=
×CE×CO×
,可得
(9-t)×4=6×4×
,
解得t=6;
当P在OA的延长线上时,
根据
×AP×AB=
×CE×CO×
,可得
(t-9)×4=6×4×
,
解得t=12;
综上所述,当t为6或12秒时,△PAE的面积等于△PCE的面积的一半;
②如图,当∠PEA=90°时,△PAE为直角三角形,过点P作PF⊥BC于F,则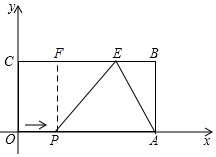
CF=OP=t,EF=6-t,BF=6-t+3=9-t=AP,
由勾股定理可得,PE2+AE2=AP2,
即(PF2+EF2)+AE2=AP2,
∴42+(6-t)2+52=(9-t)2,
解得t=
;
当∠EPA=90°时,△PAE为直角三角形,EP⊥OA,
此时,PE=OC=4,
∴Rt△APE中,AP=
=3,
∴OP=9-3=6,
∴t=6;
∵EA与AP不垂直,
∴∠PAE不可能为直角;
综上所述,当t为6或
秒时,△PAE为直角三角形.
 (1)如图,∵长方形OABC中,点B的坐标为(9,4),
(1)如图,∵长方形OABC中,点B的坐标为(9,4),∴CB=9,CO=4=AB,
又∵CE=6,
∴E(6,4),BE=3,
∵∠B=90°,
∴Rt△ABE中,AE=
| AB2+BE2 |
∴△ABE的周长:3+4+5=12;
(2)①∵OP=1×t=t,
∴AP=9-t,
∵△PAE的面积等于△PCE的面积的一半,
∴当P在OA之间时,
根据
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(9-t)×4=6×4×
| 1 |
| 2 |
解得t=6;
当P在OA的延长线上时,
根据
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(t-9)×4=6×4×
| 1 |
| 2 |
解得t=12;
综上所述,当t为6或12秒时,△PAE的面积等于△PCE的面积的一半;
②如图,当∠PEA=90°时,△PAE为直角三角形,过点P作PF⊥BC于F,则

CF=OP=t,EF=6-t,BF=6-t+3=9-t=AP,
由勾股定理可得,PE2+AE2=AP2,
即(PF2+EF2)+AE2=AP2,
∴42+(6-t)2+52=(9-t)2,
解得t=
| 2 |
| 3 |
当∠EPA=90°时,△PAE为直角三角形,EP⊥OA,
此时,PE=OC=4,
∴Rt△APE中,AP=
| AE2-PE2 |
∴OP=9-3=6,
∴t=6;
∵EA与AP不垂直,
∴∠PAE不可能为直角;
综上所述,当t为6或
| 2 |
| 3 |
看了如图,长方形OABC的顶点A、...的网友还看了以下:
AB为圆O的直径点C为圆O上一点AD和过点C的切线互相垂直垂足为点D过点C作CE垂直AB垂足为点E直 2020-03-30 …
已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.(1)如图 2020-05-13 …
三角形abc中,角acb=90°,d是bc上的点,de⊥ab于点e,且dc=de,ad与ce交于点 2020-05-17 …
自助餐和单点的英语怎么说?是英语高手就请进我在餐厅工作.餐厅的点菜方式有两种:自助餐(即付一定的钱 2020-05-21 …
如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在A 2020-06-20 …
CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC,BE=CD,CE⊥AB 2020-06-27 …
一道中考几何题求证.点B是线段AC的中点,点D是线段CE的中点,且四边形BCGF和CDHN都是正方 2020-07-20 …
如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形OD 2020-07-20 …
在△ABC中,AB=AC,AD,CE分别平分∠BAC和∠ACB,且AD与CE交于点M.点N在射线A 2020-07-21 …
如图,在△ABC中,点D、E分别在BC,AB上,连接AD,CE交于点F,点G在CE上,且DG‖AB 2020-08-02 …