已知函数f（x）=||x-2|-2|，若关于x的方程f（x）=m（m∈R）恰有四个互不相等的实根x1，x2，x3，x4，且x1<x2<x3<x4，则x1x2x3x4的取值范围是（）A.（-1，0）B.（-13，0）C.（-16，0）D.（-

Question

已知函数f（x）=||x-2|-2|，若关于x的方程f（x）=m（m∈R）恰有四个互不相等的实根x₁，x₂，x₃，x₄，且x₁<x₂<x₃<x₄，则

(x1x2)/(x3x4)的取值范围是（　　）

A. （-1，0）

B. （-

(1)/(3)，0）

C. （-

(1)/(6)，0）

D. （-

(1)/(2)，0）

Answer 1

f（x）=||x-2|-2|=

-x，x<0

x，0≤x≤2

-x+4，<x<4

x-4，x≥4

，
由图可知，若f（x）=m的四个互不相等的实数根，则m∈（0，2）
且x₁，x₂，x₃，x₄分别为：
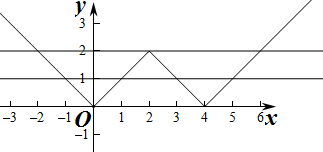
-x₁=m，x₂=m，-x₃+4=m，x₄-4=m，
即x₁=-m，x₂=m，x₃=4-m，x₄=4+m，
∴(x1x2)/(x3x4)=(-m2)/((4-m)(4+m))=(m2)/(m2-16)=1+(16)/(m2-16)，
∵m∈（0，2）
∴m²∈（0，4），m²-16∈（-16，-12）
∴(16)/(m2-16)∈（-(4)/(3)，-1），
则1+(16)/(m2-16)∈（-(1)/(3)，0），
∴(x1x2)/(x3x4)的取值范围是（-(1)/(3)，0），
故选：B．