早教吧作业答案频道 -->数学-->
如图1,Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交直线AC于D,过点C作CE⊥BD,交直线BD于E.(1)请探究线段BD与CE的数量关系.(2)在(1)中,如果把BD改为∠ABC的外角∠ABF的平分线,其他
题目详情
如图1,Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交直线AC于D,过点C作CE⊥BD,交直线BD于E.
(1)请探究线段BD与CE的数量关系.
(2)在(1)中,如果把BD改为∠ABC的外角∠ABF的平分线,其他条件均不变(如图2),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
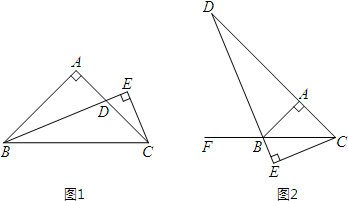
(1)请探究线段BD与CE的数量关系.
(2)在(1)中,如果把BD改为∠ABC的外角∠ABF的平分线,其他条件均不变(如图2),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.

▼优质解答
答案和解析
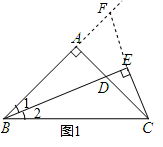 (1)BD=2CE.理由如下:
(1)BD=2CE.理由如下:
如图1,延长CE、BA交于F点,
∵CE⊥BD,交直线BD于E,
∴∠FEB=∠CEB=90°
∵BD平分∠ABC,
∴∠1=∠2,
∴∠F=∠BCF,
∴BF=BC.
∵BE⊥CF,
∴CF=2CE.
∵△ABC中,AC=AB,∠A=90°,
∴∠CBA=45°,
∴∠F=(180°-45°)÷2=67.5°,∠FBE=22.5°,
∴∠ADB=67.5°,
∵在△ADB和△AFC中,
,
∴ADB≌△AFC(AAS),
∴BD=CF,
∴BD=2CE;
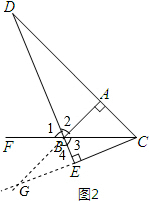
(2)结论BD=2CE仍然成立.理由如下:
如图2,延长CE、AB交于点G.
∵∠1=∠2,∠1=∠3,∠2=∠4,
∴∠3=∠4,
在△GBE与△CBE中,
∵
,
∴△GBE≌△CBE(ASA),
∴GE=CE,
∴CG=2CE.
∵∠D+∠DCG=∠G+∠DCG=90°,
∴∠D=∠G,
又∵∠DAB=∠GAC=90°,
∴△DAB∽△GAC,
∴
=
.
∵AB=AC,
∴BD=CG=2CE.
 (1)BD=2CE.理由如下:
(1)BD=2CE.理由如下:如图1,延长CE、BA交于F点,
∵CE⊥BD,交直线BD于E,
∴∠FEB=∠CEB=90°
∵BD平分∠ABC,
∴∠1=∠2,
∴∠F=∠BCF,
∴BF=BC.
∵BE⊥CF,
∴CF=2CE.
∵△ABC中,AC=AB,∠A=90°,
∴∠CBA=45°,
∴∠F=(180°-45°)÷2=67.5°,∠FBE=22.5°,
∴∠ADB=67.5°,
∵在△ADB和△AFC中,
|
∴ADB≌△AFC(AAS),
∴BD=CF,
∴BD=2CE;

(2)结论BD=2CE仍然成立.理由如下:
如图2,延长CE、AB交于点G.
∵∠1=∠2,∠1=∠3,∠2=∠4,
∴∠3=∠4,
在△GBE与△CBE中,
∵
|
∴△GBE≌△CBE(ASA),
∴GE=CE,
∴CG=2CE.
∵∠D+∠DCG=∠G+∠DCG=90°,
∴∠D=∠G,
又∵∠DAB=∠GAC=90°,
∴△DAB∽△GAC,
∴
| BD |
| CG |
| AB |
| AC |
∵AB=AC,
∴BD=CG=2CE.
看了 如图1,Rt△ABC中,∠B...的网友还看了以下:
为鉴别一株高茎豌豆是否为纯合子,最简便的方法是()A.正交B.反交C.测交D.自交 2020-05-13 …
读图,图中虚线表示回归线和极圈,关于图中内容的正确叙述是()A.XY是地轴,与黄道MN垂直B.E′ 2020-05-13 …
M(x,y)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线xx+yy=a2与该圆的位置关系 2020-05-14 …
c语言中,自然交接,交,投影和并的区别?有三个关系R、S和T如下:则由关系R和S得到关系T的操作是 2020-05-17 …
欲鉴别一株高茎豌豆是否是纯合子,最简便易行的方法是()A.杂交B.回交C.测交D.自交 2020-05-17 …
如图结构图中,框①,②处分别填入()A.l⊂α,l⊥αB.l⊂α,l与α相交C.l⊄α,l⊥αD. 2020-06-27 …
获得高产抗倒伏小麦和太空椒所采用的生物技术是()A.组织培养、无土栽培B.杂交、杂交C.杂交、转基 2020-06-27 …
1972年中日两国实现邦交正常化,其重要背景是[]A.中华人民共和国在联合国的合法权利得到恢复B. 2020-07-02 …
1972年中日两国实现邦交正常化,其重要背景是[]A.中华人民共和国在联合国的合法权利得到恢复B. 2020-07-02 …
1972年中日两国实现邦交正常化,其重要背景是[]A.中华人民共和国在联合国的合法权利得到恢复B. 2020-07-02 …