早教吧作业答案频道 -->数学-->
如图,反比例函数y=kx与y=mx交于A,B两点,设点A、B的坐标分别为A(x1,y1),B(x2,y2),S=|x1y1|,且3s-1=4s,(1)求k的值;(2)当m变化时,代数式(m2-1)x1y2(m+1)2+2x2y1m+1是否为一个固定的值?
题目详情
如图,反比例函数y=
与y=mx交于A,B两点,设点A、B的坐标分别为A(x1,y1),B(x2,y2),S=|x1y1|,且
=
,
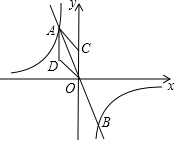
(1)求k的值;
(2)当m变化时,代数式
+
是否为一个固定的值?若是,求出其值,若不是,请说理由;
(3)点C在y轴上,点D的坐标是(-1,
),若将菱形ACOD沿x轴负方向平移m个单位,在平移过程中,若双曲线与菱形的边AD始终有交点,请直接写出m的取值范围.
| k |
| x |
| 3 |
| s-1 |
| 4 |
| s |

(1)求k的值;
(2)当m变化时,代数式
| (m2-1)x1y2 |
| (m+1)2 |
| 2x2y1 |
| m+1 |
(3)点C在y轴上,点D的坐标是(-1,
| 3 |
| 2 |
▼优质解答
答案和解析
(1)反比例函数y=
的图象在第二四象限,
∴k<0,
∵
=
,
解得:s=4,
∴k=-|x1y1|=-s=-4,
(2)∵反比例函数的图象是关于原点O的中心对称图形,
∴OA=OB,
∴x1=-x2,y1=-y2,
∴x1y2=x2y1,
+
=
(m2-1+2m+2)=x2y1=x2•(-
)=4,
∴代数式是否为一个固定的值4;
(3)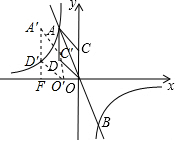 如图,
如图,
将菱形ACOD沿x轴负方向平移m个单位,
使得点D′落在反比例函数y=-
的图象的D'处,
过点D'做x轴的垂线,垂足为F,
∵D的坐标是(-1,
),
∴D'(-1-m,
),
∴点D'的纵坐标为3,
∵D'落在函数y=-
(x<0)的图象上,
∴
=-
,
∴x=-
,
∴-1-m=-
,
∴m=
,
∴m的取值范围:0≤m≤
.
| k |
| x |
∴k<0,
∵
| 3 |
| s-1 |
| 4 |
| s |
解得:s=4,
∴k=-|x1y1|=-s=-4,
(2)∵反比例函数的图象是关于原点O的中心对称图形,
∴OA=OB,
∴x1=-x2,y1=-y2,
∴x1y2=x2y1,
| (m2-1)x1y2 |
| (m+1)2 |
| 2x2y1 |
| m+1 |
| x1y2 |
| (m+1)2 |
| 4 |
| x1 |
∴代数式是否为一个固定的值4;
(3)
 如图,
如图,将菱形ACOD沿x轴负方向平移m个单位,
使得点D′落在反比例函数y=-
| 4 |
| x |
过点D'做x轴的垂线,垂足为F,
∵D的坐标是(-1,
| 3 |
| 2 |
∴D'(-1-m,
| 3 |
| 2 |
∴点D'的纵坐标为3,
∵D'落在函数y=-
| 4 |
| x |
∴
| 3 |
| 2 |
| 4 |
| x |
∴x=-
| 8 |
| 3 |
∴-1-m=-
| 8 |
| 3 |
∴m=
| 5 |
| 3 |
∴m的取值范围:0≤m≤
| 5 |
| 3 |
看了 如图,反比例函数y=kx与y...的网友还看了以下:
1方程x^2+2x+1=0的根为X1= X2= X1+X2= X1X2= 方程x^2-3x-1=0 2020-05-16 …
抛物线y=ax2与直线y=kx+b(k≠0)交于A,B两点,且此两点的横坐标分别为x1,x2,直线 2020-05-17 …
某人骑摩托车由静止从A地沿平直公路经经小村庄驶向并停在D地,B、C为小村庄的两个村口,AD总位移为 2020-07-19 …
若一元二次方程ax²+bx+c=0(a≠0)的两个实数根为x1,x2,那么二次三项式ax²+bx+ 2020-07-31 …
先阅读下面的材料,然后解答问题.通过计算,发现方程:x+1x=2+12的解为x1=2,x2=12;x 2020-10-31 …
已知关于x的方程kx=sinx(k为正常数)在区间(-3π,3π)内有且仅有5个实数根,从小到大依次 2020-10-31 …
已知一元二次方程x2-x-3=0的较小根为x1,则下面对x1的估计正确的是()A.-2<x1<-1B 2020-11-12 …
(2014•德阳一模)已知A、B、C三点同在直线l上,点O不在l上,且OA=(1+xlnx)OB-( 2020-11-12 …
在y=(1/2)的x次方,y=log2x,y=x2这三个函数中,当0<x1<x2<1时,使f(括号里 2020-12-08 …
很难的二次函数题,已知二次函数y=kx^2+(2k-1)x-1与x轴交点的横坐标分别为x1和x2(x 2020-12-23 …