早教吧作业答案频道 -->数学-->
函数的图象关于直线对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是.
题目详情
函数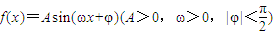 的图象关于直线
的图象关于直线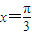 对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
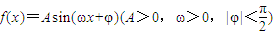 的图象关于直线
的图象关于直线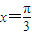 对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 . ▼优质解答
答案和解析
【答案】 分析: 先根据函数的最小正周期求出ω的值,因为函数的对称轴为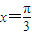 ,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
函数f(x)=Asin(ωx+∅)的周期T=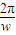 =π,∴ω=2
=π,∴ω=2
∵函数f(x)=Asin(2x+∅)的图象关于直线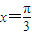 对称,∴f(0)=f(
对称,∴f(0)=f(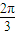 )
)
即Asin∅=Asin(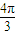 +∅),化简得,sin∅=-
+∅),化简得,sin∅=-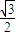 cos∅-
cos∅- sinφ
sinφ
 sin∅=-
sin∅=-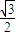 cos∅,tan∅=-
cos∅,tan∅=-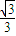 ,
,
又∵|∅|<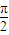 ,∴∅=-
,∴∅=-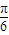 ,∴f(x)=Asin(2x-
,∴f(x)=Asin(2x-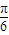 )
)
令2x-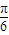 =kπ,k∈Z,解得,x=
=kπ,k∈Z,解得,x=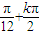 ,k∈Z,
,k∈Z,
∴函数y=f(x)图象的对称中心是(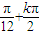 ,0),k∈Z
,0),k∈Z
其中,离坐标原点O最近的对称中心是(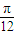 ,0)
,0)
故答案为(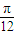 ,0)
,0)
点评: 本题主要考查y=Asin(ωx+∅)的图象与性质,解题时借助基本的正弦函数的图象和性质.
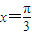 ,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.函数f(x)=Asin(ωx+∅)的周期T=
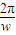 =π,∴ω=2
=π,∴ω=2∵函数f(x)=Asin(2x+∅)的图象关于直线
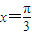 对称,∴f(0)=f(
对称,∴f(0)=f(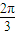 )
)即Asin∅=Asin(
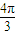 +∅),化简得,sin∅=-
+∅),化简得,sin∅=-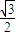 cos∅-
cos∅- sinφ
sinφ sin∅=-
sin∅=-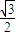 cos∅,tan∅=-
cos∅,tan∅=-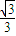 ,
,又∵|∅|<
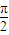 ,∴∅=-
,∴∅=-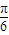 ,∴f(x)=Asin(2x-
,∴f(x)=Asin(2x-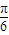 )
)令2x-
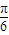 =kπ,k∈Z,解得,x=
=kπ,k∈Z,解得,x=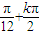 ,k∈Z,
,k∈Z,∴函数y=f(x)图象的对称中心是(
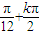 ,0),k∈Z
,0),k∈Z其中,离坐标原点O最近的对称中心是(
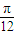 ,0)
,0)故答案为(
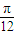 ,0)
,0)点评: 本题主要考查y=Asin(ωx+∅)的图象与性质,解题时借助基本的正弦函数的图象和性质.
看了 函数的图象关于直线对称,它的...的网友还看了以下:
已知X={-1,0,1},Y={-2,-1,0,1,2},射影f:X到Y满足:对任意的x属于X,它 2020-05-13 …
设函数y=(2x-3)/(x+2)给出下列命题:正确的是①fx图象可由反比例函数y=-7/x经平变 2020-05-14 …
在研究反比例函数y=ax(a≠0)的图象时,我们发现有如下性质:(1)图象是中心对称图形,对称中心 2020-05-16 …
已知二次函数y=x²-(m-1)x+m²-2m-3,其中m为实数,若其图象过原点求函数式(1)同上 2020-06-14 …
点m(x,y)在第一象限,它的坐标满足x+2y=m+2,4x+5y=6m+3,并且x>y点M(x, 2020-06-24 …
已知原象(x,y)在映射f下的象是(x+y,x-y)则(2,-3)的原象是和这题已知(x,y)在映 2020-07-30 …
1、已知y=y1y2,其中y1=k/x(k≠0的常数),y2与x的平方成正比例,求证y与x也成正比 2020-08-03 …
已知函数y=x+x-1,其图象如图.给出下列几个命题:①该函数的图象是中心对称图形;②y的值不可能 2020-08-03 …
链接中考诗歌意象意象即带有诗人主观情感的客观物象,它可以是自然景象,也可以是人文景象。作者要通过意象 2020-11-05 …
自尊是一种常见的心理现象,它的含义是()A.是一种常见的心理现象,即轻视看不起别人B.就是尊重他人C 2020-12-03 …