早教吧作业答案频道 -->数学-->
课堂上,某老师给出一道数学题:如图1所示,D点在AB上,E点在AC的延长线上,且BD=CE,连接DE交BC于F,若F点是DE的中点,证明:AB=AC.小明的思路是:过D作DG∥AE,交BC于点G,如图2;小丽的思
题目详情
课堂上,某老师给出一道数学题:如图1所示,D点在AB上,E点在AC的延长线上,且BD=CE,连接DE交BC于F,若F点是DE的中点,证明:AB=AC.
小明的思路是:过D作DG∥AE,交BC于点G,如图2;
小丽的思路是过E作EH∥AB,交BC的延长线于点H,如图3.
请根据小明或小丽的思路任选一种完成该题的证明过程.
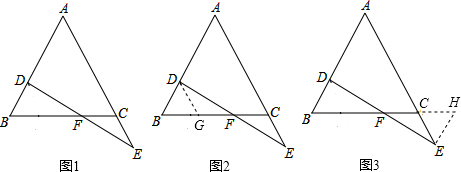
小明的思路是:过D作DG∥AE,交BC于点G,如图2;
小丽的思路是过E作EH∥AB,交BC的延长线于点H,如图3.
请根据小明或小丽的思路任选一种完成该题的证明过程.

▼优质解答
答案和解析
证明:图2,∵DG∥AE,
∴∠DGF=∠ECF,∠GDF=∠E,
∵F点是DE的中点,
∴DF=EF,
∵在△DFG和△EFC中
∴△DFG≌△EFC(AAS),
∴DG=CE,
∵BD=CE,
∴BD=DG,
∴∠B=∠DGB,
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠B=∠ACB,
∴AB=AC;
图3,∵EH∥AB,
∴∠B=∠H,
在△BDF和△HEF中
∴△BDF≌△HEF(AAS),
∴EH=BD,
∵BD=CE,
∴CE=EH,
∴∠H=∠HCE,
∵∠H=∠B,∠HCE=∠ACB,
∴∠B=∠ACB,
∴AB=AC.
∴∠DGF=∠ECF,∠GDF=∠E,
∵F点是DE的中点,
∴DF=EF,
∵在△DFG和△EFC中
|
∴△DFG≌△EFC(AAS),
∴DG=CE,
∵BD=CE,
∴BD=DG,
∴∠B=∠DGB,
∵DG∥AE,
∴∠DGB=∠ACB,
∴∠B=∠ACB,
∴AB=AC;
图3,∵EH∥AB,
∴∠B=∠H,
在△BDF和△HEF中
|
∴△BDF≌△HEF(AAS),
∴EH=BD,
∵BD=CE,
∴CE=EH,
∴∠H=∠HCE,
∵∠H=∠B,∠HCE=∠ACB,
∴∠B=∠ACB,
∴AB=AC.
看了 课堂上,某老师给出一道数学题...的网友还看了以下:
在直角坐标系内,点A在x轴正半轴上,点B在y轴负半轴上,且A点与原点的距离为B点与原点距离的2倍, 2020-05-16 …
正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标 2020-05-16 …
如图①,点A(a,6)在第一象限,点B(0,b)在y轴负半轴上,且a、b满足(a-4)2+|b-4 2020-06-04 …
如图,数a,bc对应的点在数轴上,且a、b互为相反数(1)a+b0,c-b0,a-c0.(2)/a 2020-07-09 …
已知抛物线y=ax²-2ax-3与x轴交于A(-1,0)和B两点,与y轴交于点c,其顶点为M.1, 2020-07-18 …
在三角形ABC中,AB=AC,将三角形ABC绕点B旋转到三角形A'BC'的位置,使点A在BC上,且 2020-07-22 …
分子式为C9H8O4的物质A有苯环,苯环上的两个取代基连在相邻的碳原子上,且A和NaOH溶液反应生成 2020-10-31 …
若A(a,b)B(a-2,c)两点均在函数y=1/x的图像上且a小于0则b与c的大小关系为()若A( 2020-12-12 …
正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴上,且A的坐标是(1,0) 2020-12-25 …
C岛在A岛的北偏东50度方向上,B岛在C岛的南偏西10度方向上,且A岛在B岛的北偏西70度方向上,求 2021-01-02 …