如图是函数图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有，则（）A．f（x）在上是减函数B．f（x）在上是减函数C．f（x）在上是增函数D．f（x）在上是减函

Question

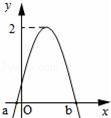
如图是函数图象的一部分，对不同的x₁，x₂∈[a，b]，若 f（x₁）=f（x₂），有，则（　　）

A．f（x）在上是减函数   B．f（x）在上是减函数

C．f（x）在上是增函数   D．f（x）在上是减函数

Answer 1

C【考点】正弦函数的图象．

【专题】三角函数的图像与性质．

【分析】由条件根据函数y=Asin（ωx+φ）的图象特征，求得a+b=﹣φ，再根据f（a+b）=2sinφ=，求得φ的值，可得f（x）的解析式，再根据正弦函数的单调性得出结论．

【解答】由函数图象的一部分，可得A=2，函数的图象关于直线x==对称，∴a+b=x₁+x₂．

由五点法作图可得2a+φ=0，2b+φ=π，∴a+b=﹣φ．

再根据f（a+b）=2sin（π﹣2φ+φ）=2sinφ=，可得sinφ=，

∴φ=，f（x）=2sin（2x+）．

在上，2x+∈（﹣，），故f（x）在上是增函数，

故选：C．

【点评】本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象特征，正弦函数的单调性，属于中档题．