已知AB是抛物线x2=2py(p＞0)的任一弦，F为抛物线的焦点，l为准线，m为过A点且以v=(0-1)为方向向量的直线.(1)若过A点的抛物线的切线与y轴相交于C点，求证：|AF|=|CF|；(2)若·+p2

Question

已知AB是抛物线x ² =2py(p＞0)的任一弦，F为抛物线的焦点，l为准线，m为过A点且以v=(0 -1)为方向向量的直线.

(1)若过A点的抛物线的切线与y轴相交于C点，求证：|AF|=|CF|；

(2)若 · +p ² =0(A、B异于原点)，直线OB与m相交于点P，试求P点的轨迹方程；

(3)若AB为焦点弦，分别过A、B点的抛物线的两条切线相交于点T，求证：AT⊥BT，且T点在l上.

Answer 1

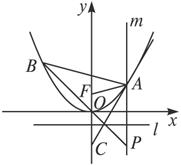
(1)证明：如图，设A(x ₁ y ₁ )

    ∵y′=

    ∴k _AC = .

    于是AC的方程为y-y ₁ = (x-x ₁ ) 即y= x-y ₁ .

    令x=0，得y=-y ₁ 即C(0，-y ₁ ).

    由定义，|AF|=y ₁ + .

    又|CF|= -(-y ₁ )=y ₁ +

    故|AF|=|CF|.

    (2)设A(x ₁ y ₁ ) B(x ₂ y ₂ ) P(x y)

    · +p ² =0 x ₁ x ₂ +y ₁ y ₂ +p ² =0 x ₁ x ₂ + +p ² =0 ( +p) ² =0.

    ∴x ₁ x ₂ =-2p ² .

    直线OB的方程为y= x= x           ①

    直线m的方程为x=x ₁                            ②

    ①×②得xy= x xy+px=0

    ∵x≠0 ∴y=-p.

    故P点的轨迹方程为y=-p.

(3)证明：设A(x ₁ y ₁ )、B(x ₂ y ₂ )、T(x ₀ y ₀ ) 则k _AT = k _BT = .

    由于AB是焦点弦，可设AB的方程为y=kx+ ，代入x ² =2py 得x ² -2pkx-p ² =0.∴x ₁ x ₂ =-p ² .

    于是k _AT ·k _BT = =-1 故AT⊥BT.

    由(1)知，AT的方程为y= x-y ₁

    ∴y ₀ = x ₀ -y ₁ 即x ₀ x ₁ -py ₁ =py ₀ .

    同理 x ₀ x ₂ -py ₂ =py ₀

    ∴AB的方程为x ₀ x-py=py ₀ .

    又∵AB过焦点，∴- =py ₀ 即y ₀ =- .

    故T点在准线l上.