早教吧作业答案频道 -->数学-->
如图,点C是以AB为直径的O上一点,CD是O切线,D在AB的延长线上,作AE⊥CD于E.(1)求证:AC平分∠BAE;(2)若AC=2CE=6,求O的半径;(3)请探索:线段AD,BD,CD之间有何数量关系?请证明
题目详情
如图,点C是以AB为直径的 O上一点,CD是 O切线,D在AB的延长线上,作AE⊥CD于E.
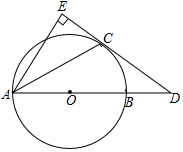
(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求 O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?请证明你的结论.

(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求 O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?请证明你的结论.
▼优质解答
答案和解析
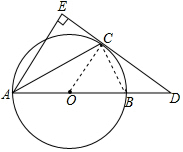 (1)证明:连接OC,
(1)证明:连接OC,
∵CD是 O切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠EAC=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠EAC=∠A=CAO,
即AC平分∠BAE;
(2) 连接BC,
∵AE⊥CE,AC=2CE=6,
∴sin∠CAE=
=
,
∴∠CAE=30°,
∴∠CAB=∠CAE=30°,
∵AB是 O的直径,
∴∠ACB=90°,
∴cos∠CAB=
=
,
∴AB=4
,
∴ O的半径是2
;
(3)CD2=BD•AD,
证明:∵∠DCB+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠DCB=∠ACO,
∴∠DCB=∠ACO=∠CAD,
∵∠D=∠D,
∴△BCD∽△CAD,
∴
=
,
即CD2=BD•AD.
 (1)证明:连接OC,
(1)证明:连接OC,∵CD是 O切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠EAC=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠EAC=∠A=CAO,
即AC平分∠BAE;
(2) 连接BC,
∵AE⊥CE,AC=2CE=6,
∴sin∠CAE=
| CE |
| AC |
| 1 |
| 2 |
∴∠CAE=30°,
∴∠CAB=∠CAE=30°,
∵AB是 O的直径,
∴∠ACB=90°,
∴cos∠CAB=
| AC |
| AB |
| ||
| 2 |
∴AB=4
| 3 |
∴ O的半径是2
| 3 |
(3)CD2=BD•AD,
证明:∵∠DCB+∠BCO=90°,∠ACO+∠BCO=90°,
∴∠DCB=∠ACO,
∴∠DCB=∠ACO=∠CAD,
∵∠D=∠D,
∴△BCD∽△CAD,
∴
| BD |
| CD |
| CD |
| AD |
即CD2=BD•AD.
看了 如图,点C是以AB为直径的O...的网友还看了以下:
作文心灵的绳索急求一篇关于心灵的绳索作文 700字左右 2020-05-15 …
编动物检索表求高手帮忙用鳞翅目、螳螂目、半翅目、同翅目、直翅目、膜翅目、双翅目做一份检索表. 2020-06-03 …
阅读短文,《给予》金波都说童年是索取的时代想索取夜空的星辰,想索取早晨的彩云,童年里我索取过多少关 2020-06-24 …
EI数据库使用的位置算符、截词算符分别有哪几种?EI数据库在高级检索方式中,字段检索用什么形式?若 2020-06-26 …
用“/”给文言文阅读材料中加波浪线的句子断句。然天下之境涉而即得得而辄尽者始焉欣欣继焉索索欲求余味 2020-07-11 …
EI检索号求助发表在EnergyProcedia最好能给我说一下检索方法,在哪儿检索的.杂志名称E 2020-08-03 …
(路漫漫其修远兮,吾将上下为求索)求改编.(路漫漫其修远兮,吾将上下为求索)求改编. 2020-11-23 …
练习写书评,培养和提升鉴赏与表达能力评论《智取生辰纲》的两条线索[要求]①自拟题目,这个标题最好能代 2020-12-19 …
人肉搜索可以在最短时间内揭露某某门背后的真相,为某某找到大众认可的道德定位,但其追求的最高目标是:不 2020-12-21 …
pubmed练习题从MeSH途径搜索麻疹爆发文献线索要求写出步骤 2020-12-22 …