早教吧作业答案频道 -->数学-->
七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公理化化思想.请完成下列
题目详情
七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公理化化思想.请完成下列证明活动:
活动1.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)已知:如图1,直线AB、CD被直线EF所截,AB∥CD.
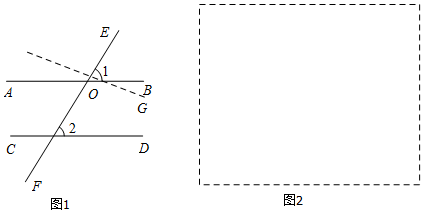
求证:∠1=∠2.
证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
∵∠EOG=∠2,
∴OG∥CD(___).
∴过O点存在两条直线AB、OG两条直线与CD平行,这与基本事实(___)矛盾.
∴假设不成立.
∴∠1=∠2.
活动2.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:___.
求证:___.
证明:
活动1.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)已知:如图1,直线AB、CD被直线EF所截,AB∥CD.

求证:∠1=∠2.
证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
∵∠EOG=∠2,
∴OG∥CD(___).
∴过O点存在两条直线AB、OG两条直线与CD平行,这与基本事实(___)矛盾.
∴假设不成立.
∴∠1=∠2.
活动2.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:___.
求证:___.
证明:
▼优质解答
答案和解析
 活动1,证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
活动1,证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
∵∠EOG=∠2,
∴OG∥CD(同位角相等,两直线平行).
∴过O点存在两条直线AB、OG两条直线与CD平行,这与基本事实(AB∥CD)矛盾.
∴假设不成立.
∴∠1=∠2.
故答案为:同位角相等,两直线平行,AB∥CD;
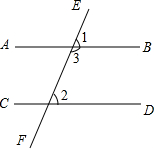
活动2,已知:AB∥CD,
求证:两直线平行,同旁内角互补.
证明:如图,∵AB∥CD,
∴∠1=∠2.
∵∠1+∠3=180°,
∴∠2+∠3=180°,即两直线平行,同旁内角互补.
故答案为:AB∥CD,两直线平行,同旁内角互补,
 活动1,证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
活动1,证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.∵∠EOG=∠2,
∴OG∥CD(同位角相等,两直线平行).
∴过O点存在两条直线AB、OG两条直线与CD平行,这与基本事实(AB∥CD)矛盾.
∴假设不成立.
∴∠1=∠2.
故答案为:同位角相等,两直线平行,AB∥CD;
活动2,已知:AB∥CD,
求证:两直线平行,同旁内角互补.
证明:如图,∵AB∥CD,
∴∠1=∠2.
∵∠1+∠3=180°,
∴∠2+∠3=180°,即两直线平行,同旁内角互补.
故答案为:AB∥CD,两直线平行,同旁内角互补,
看了 七年级教材在图形与几何部分给...的网友还看了以下:
有关图中蛋白质的叙述,正确的是()A.此蛋白质的R基中共含有22个氨基B.共有95个肽键C.形成此 2020-04-07 …
下列有关图中某蛋白质的叙述,不正确的是()A.该蛋白质含有两条肽链B.该蛋白质共有128个肽键C. 2020-05-13 …
蛋白质和氨基酸的计算题加选择题一个蛋白质分子有两条肽链构成,共有226个氨基酸组成,则这个蛋白质分 2020-05-17 …
生物钟的蛋白质相对分子质量=氨基酸平均分子质量×氨基酸减18×(氨基酸-肽链数)这条式子怎样来的 2020-05-23 …
有关图示中蛋白质的叙述,正确的是()A.形成该蛋白质时共脱掉126个水分子B.该蛋白质含有两条肽链 2020-07-08 …
七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的 2020-07-30 …
多糖或糖基合成的顺序怎么控制?糖蛋白等物质的糖基有严格且固定的单糖顺序,请问怎么调控或者编码?我问得 2020-11-28 …
下列关于蛋白质的结构和功能的叙述,正确的是()A.组成蛋白质的氨基酸之间可按不同的方式相互结合B.蛋 2021-01-13 …
组成某蛋白质的氨基酸的R基中无游离的氨基和羧基,经实验测的该蛋白质分子共有3个游离的氨基和3个羧基那 2021-01-13 …
如图为某蛋白质的相关信息,下列叙述不正确的是()A.合成该蛋白质的场所为核糖体B.该蛋白质含有两条肽 2021-01-13 …