早教吧作业答案频道 -->数学-->
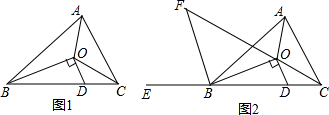
△ABC中,三个内角的平分线交于点O,过点O作OD⊥OB,交边BC于点D.(1)如图1,猜想∠AOC与∠ODC的关系,并说明你的理由;(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.①求证:
题目详情
△ABC中,三个内角的平分线交于点O,过点O作OD⊥OB,交边BC于点D.
(1)如图1,猜想∠AOC与∠ODC的关系,并说明你的理由;
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.
①求证:BF∥OD;
②若∠F=35°,求∠BAC的度数.
(1)如图1,猜想∠AOC与∠ODC的关系,并说明你的理由;
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.
①求证:BF∥OD;
②若∠F=35°,求∠BAC的度数.

▼优质解答
答案和解析
(1)∠AOC=∠ODC,
理由:∵三个内角的平分线交于点O,
∴∠OAC+∠OCA=
(∠BAC+∠BCA)=
(180°-∠ABC),
∵∠OBC=
∠ABC,
∴∠AOC=180°-(∠OAC+∠OCA)=90°+
∠ABC=90°+∠OBC,
∵OD⊥OB,
∴∠BOD=90°,
∴∠ODC=90°+∠OBD,
∴∠AOC=∠ODC;
(2)①∵BF平分∠ABE,
∴∠EBF=
∠ABE=
(180°-∠ABC)=90°-∠DBO,
∵∠ODB=90°-∠OBD,
∴∠FBE=∠ODB,
∴BF∥OD;
②∵BF平分∠ABE,
∴∠FBE=
ABE=
(∠BAC+∠ACB),
∵三个内角的平分线交于点O,
∴∠FCB=
ACB,
∵∠F=∠FBE-∠BCF=
(∠BAC+∠ACB)-
∠ACB=
BAC,
∵∠F=35°,
∴∠BAC=2∠F=70°.
理由:∵三个内角的平分线交于点O,
∴∠OAC+∠OCA=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OBC=
| 1 |
| 2 |
∴∠AOC=180°-(∠OAC+∠OCA)=90°+
| 1 |
| 2 |
∵OD⊥OB,
∴∠BOD=90°,
∴∠ODC=90°+∠OBD,
∴∠AOC=∠ODC;
(2)①∵BF平分∠ABE,
∴∠EBF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ODB=90°-∠OBD,
∴∠FBE=∠ODB,
∴BF∥OD;
②∵BF平分∠ABE,
∴∠FBE=
| 1 |
| 2 |
| 1 |
| 2 |
∵三个内角的平分线交于点O,
∴∠FCB=
| 1 |
| 2 |
∵∠F=∠FBE-∠BCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠F=35°,
∴∠BAC=2∠F=70°.
看了 △ABC中,三个内角的平分线...的网友还看了以下:
如图,平行四边形ABCD 的对角线AC与BD相交于点0,直线EF过点0,且与AB、DC分别相交于点 2020-05-16 …
直线Y=-4\3X+6分别于X轴Y轴交于AB两点直线Y=4/5x于AB教育点C于过点A且平行于Y轴 2020-06-15 …
△ABC是等边三角形,D是边AC上一点,BD的垂直平分线交边AB于点E,交边BC于点F△ABC是等 2020-06-23 …
如图,AB,BC,CD分别于圆O相切于E,F,G,且AB平行于CD,OB于EF相交于M,OC与FG 2020-07-24 …
在三角形ABC中,点O是AC边上的一个动点,过点O作MN平行于BC,交角ACB的平分线于点E,交角 2020-07-30 …
如图在三角形ABC中,点O是AC边上的动点,过点O作直线EF//BC,交于角BCA的平分线于点E, 2020-07-30 …
1ab等于ac,角a等于36度,ab得中垂线mn交ac于点d,交ab于点m,求证bd是角abc的平 2020-07-30 …
三角形abc的内角abc和外角ac的角平分线交于点e,be交ac于f,过点e做eg平行于bd交a三 2020-07-31 …
在三角形ABC中,角B=22.5度,AB的垂直平分线交AB于点Q,交BC于点P,PE垂直AC,垂足 2020-08-03 …
已知AB平行CD,角ABP和角CD的平分线相交于点E角ABE和角CDE的平分线相交于点F已知AB平行 2020-11-03 …