早教吧作业答案频道 -->数学-->
如图,在射线BA、BC、AD、CD围成的菱形ABCD中,∠ABC=60°,AB=63,O是射线BD上一点,O与BA、BC都相切、与BO的延长线交于点M.过M作EF⊥BD交线段BA(或线段AD)于点E、交线段BC(或线段CD)于点F.
题目详情
如图,在射线BA、BC、AD、CD围成的菱形ABCD中,∠ABC=60°,AB=6
,O是射线BD上一点, O与BA、BC都相切、与BO的延长线交于点M.过M作EF⊥BD交线段BA(或线段AD)于点E、交线段BC(或线段CD)于点F.以EF为边作矩形EFGH,点G、H分别在围成菱形的另外两条线段上.
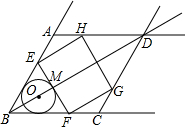
(1)求证:BO=2OM;
(2)当矩形EFGH的面积为24
时,求 O的半径.
| 3 |

(1)求证:BO=2OM;
(2)当矩形EFGH的面积为24
| 3 |
▼优质解答
答案和解析
(1)如图1所示:设 O切AB于点P,连接OP,则∠OPB=90°.
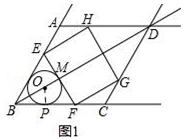
∵四边形ABCD为菱形,
∴∠ABD=
∠ABC=30°.
∴OB=2OP.
∵OP=OM,
∴BO=2OP=2OM.
(2)如图2所示:设GH交BD于点N,连接AC,交BD于点Q.
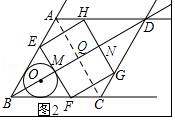
∵四边形ABCD是菱形,
∴AC⊥BD.
∴BD=2BQ=
AB=18.
设 O的半径为r,则OB=2r,MB=3r.
①如图2所示,当点E在AB上时.
在Rt△BEM中,EM=
r.由对称性得:EF=2EM=2
r,ND=BM=3r.
∴MN=18-6r.
∴S矩形EFGH=EF•MN=2
r(18-6r)=24
.
解得:r1=1,r2=2.
如图3所示:
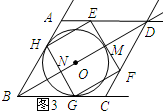
点E在AD边上时.BM=3r,则MD=18-3r.
由对称性可知:NB=MD=6.(根据图2知),
∴MB=3r=18-6=12.
解得:r=4.
综上所述, O的半径为1或2或4.

∵四边形ABCD为菱形,
∴∠ABD=
| 1 |
| 2 |
∴OB=2OP.
∵OP=OM,
∴BO=2OP=2OM.
(2)如图2所示:设GH交BD于点N,连接AC,交BD于点Q.

∵四边形ABCD是菱形,
∴AC⊥BD.
∴BD=2BQ=
| 3 |
设 O的半径为r,则OB=2r,MB=3r.
①如图2所示,当点E在AB上时.
在Rt△BEM中,EM=
| 3 |
| 3 |
∴MN=18-6r.
∴S矩形EFGH=EF•MN=2
| 3 |
| 3 |
解得:r1=1,r2=2.
如图3所示:

点E在AD边上时.BM=3r,则MD=18-3r.
由对称性可知:NB=MD=6.(根据图2知),
∴MB=3r=18-6=12.
解得:r=4.
综上所述, O的半径为1或2或4.
看了 如图,在射线BA、BC、AD...的网友还看了以下:
两个等量异种电荷连线的中点为O,则在该连线的中垂线上,O点的场强是否最强?为什么(求详...两个等 2020-06-06 …
(2013•重庆)设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1 2020-06-16 …
假设在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中,有一条曲线L,使沿该曲线从 2020-06-22 …
在△ABC中,AD是中线,O为AD的中点,直线a过点O,过A、B、C三点分别作直线a的垂线,垂足分 2020-06-22 …
在△ABC中,AD是中线,O为AD的中点,直线a过点O,过A、B、C三点分别作直线a的垂线,垂足分 2020-06-22 …
(2011•成都)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经 2020-07-22 …
正方形ABCD中,O为对角线AC的中点,P为AC上一点,连接BP,过点P作BP⊥PE,PE交直线C 2020-07-24 …
我们规定:若点O是线段MN4中点,则称点M关于O4对称点是N(或称点M与点N关于O成中心对称);若 2020-08-01 …
如图所示,在真空中的绝缘水平面上,两相距为2L的固定的同种点电荷A、B带电量均为+Q,O点为两电荷连 2020-12-05 …
下列各句中,加线成语中使用恰当的一句是[]A.各国游客在北京每到一处都能感受到中国老百姓的热情,大家 2020-12-15 …