早教吧作业答案频道 -->数学-->
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F
题目详情
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴___=___(___).
同理可得,PB=___.
∴___=___(等量代换).
∴___(到一条线段两个端点距离相等的点,在这条线段的___)
∴AB、BC、AC的垂直平分线相交于点P,且___.
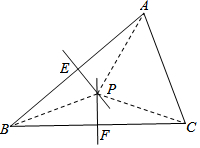
已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴___=___(___).
同理可得,PB=___.
∴___=___(等量代换).
∴___(到一条线段两个端点距离相等的点,在这条线段的___)
∴AB、BC、AC的垂直平分线相交于点P,且___.

▼优质解答
答案和解析
 证明:∵点P是AB边垂直平线上的一点,
证明:∵点P是AB边垂直平线上的一点,
∴PB=PA (垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
∴AB、BC、AC的垂直平分线相交于点P,且PA=PB=PC.
故答案为:PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;PA;PC;点P在AC的垂直平分线上,垂直平分线上;PA=PB=PC.
 证明:∵点P是AB边垂直平线上的一点,
证明:∵点P是AB边垂直平线上的一点,∴PB=PA (垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
∴AB、BC、AC的垂直平分线相交于点P,且PA=PB=PC.
故答案为:PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;PA;PC;点P在AC的垂直平分线上,垂直平分线上;PA=PB=PC.
看了 证明定理:三角形三条边的垂直...的网友还看了以下:
在等边三角形ABC中,D为线段BC上的动点,连接AD,在角ADC内作角ADE等于60度,交AC边于 2020-05-13 …
把三角尺放在边长1的正方形ABCD上,使直角顶点P在对角线AC上滑动,直角边始终过点B,另一边与射 2020-05-16 …
过M边形一个顶点有七条对顶线,N边形没有对顶线,K边形有K角对角线,求(M-k)的n次方的值是多少 2020-05-23 …
下列结论正确的是()A.对角线相等且一组对角相等的四边形是平行四边形B.一边长为5cm,两条对角线 2020-06-13 …
有这样一道物理题,说是水平面有一个宽度为d(d>L)的磁场,方向竖直向上,磁感应强度强度B,质量为 2020-07-03 …
关于对角线一M边没有对角线,N边形共有5条对角线,则M-N等于几?二多边形的一个顶点的所有对角线把 2020-07-13 …
如图,空间某区域中有一匀强磁场,磁感应强度方向水平,且垂直于纸面向里,磁场上边界b和下边界d水平。 2020-07-22 …
如图所示,点A、O、B在同一条直线上,∠AOC=1/2∠BOC+30°,OE平分∠BOC,求BOE 2020-08-02 …
如图所示,点A、O、B在同一条直线上,∠AOC=1/2∠BOC+30°,OE平分∠BOC,求BOE 2020-08-02 …
在下列命题中,正确的是()A.正多边形一个内角与一个外角相等,则它是正六边形B.正多边形都是中心对 2020-08-02 …