早教吧作业答案频道 -->数学-->
已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.(1)如图1,线段EH、CH、AE之间的数量关系是;(2)如图2,将△DHE绕点D顺时
题目详情
已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是___;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
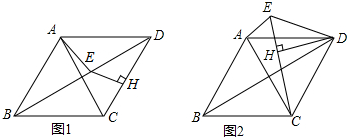
(1)如图1,线段EH、CH、AE之间的数量关系是___;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.

▼优质解答
答案和解析
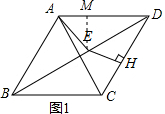 (1)EH2+CH2=AE2,
(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,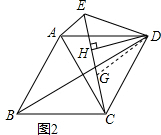
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG-∠ADG=∠ADC-∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.
 (1)EH2+CH2=AE2,
(1)EH2+CH2=AE2,如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
|
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,

∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG-∠ADG=∠ADC-∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
|
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.
看了 已知,在菱形ABCD中,∠A...的网友还看了以下:
右图表示某植物生长与温度的关系,由图可知6.右图表示某植物生长与温度的关系,由图可知22.jpg( 2020-04-27 …
在一定温度下,两个电路元件A和B的电流和电压关系如图所示.由图可知,元件(选:A/B)的电流与它两 2020-05-14 …
如图所示是一把技能吹冷风、又能吹热风的简化电路图其中M是吹风机,R是电热丝.由电路图可知()A.只 2020-07-15 …
如图所示是描述原子核核子的平均质量.m与原子序数Z的关系曲线,由图可知下列说法正确的是()A.将原 2020-07-20 …
图甲是用伏安法测未知电阻R的实验图.(1)请用笔画线代替导线,将图甲中实物电路连接完整.(2)闭合 2020-07-21 …
如图,已知三角形ABC将BC边上一点P(点BC除外)向上移动,使BP平分角B,CP平分角C,探究角 2020-07-21 …
如图所示,图甲为一个电灯泡两端电压与通过它的电流的变化关系曲线.由图可知,两者不成线性关系,这是由于 2020-11-02 …
如图是关于电阻A、B的I-U图象.由图可知,电阻值分别是Ω和Ω.若将A、B两电阻并联后接在电压为2V 2020-11-03 …
matlab中关于含参函数的矩阵绘图已知y=y(i),x=x(i),如何在一张图里绘制y关于x的点; 2020-12-12 …
如图甲是用伏安法测未知电阻R的实验图.(1)请用笔画线代替导线,将图甲中实物电路连接完整.(2)闭合 2021-01-22 …