早教吧作业答案频道 -->数学-->
如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD(1)求证;四边形OBFE是平行四边形;(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?
题目详情
如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD
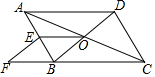
(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD

(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.


(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD

(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.

▼优质解答
答案和解析
(1)证明:四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB中点,
∴AE=BE
∴OE为△ABC的中位线,
∴OE∥BC,
∵EF∥BD,
∴四边形OBFE是平行四边形.
(2)结论:当AD⊥BD时,四边形OBFE是矩形
∵四边形ABCD是平行四边形,
∴OB=OD
∵E为AB中点,
∴AE=BE
∴OE为△ABD的中位线,
∴OE∥AD,
∴∠BOE=∠BDA,
∵AD⊥BD,
∴∠BOE=BDA=90°,
∵四边形OBFE是平行四边形,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.
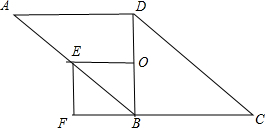
理由:∵OE为△ABD的中位线,
∴OE=
AD
∵O为BD中点,
∴OB=
BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
1 2 1 1 12 2 2AD
∵O为BD中点,
∴OB=
BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
1 2 1 1 12 2 2BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
∴OA=OC,
∵E为AB中点,
∴AE=BE
∴OE为△ABC的中位线,
∴OE∥BC,
∵EF∥BD,
∴四边形OBFE是平行四边形.
(2)结论:当AD⊥BD时,四边形OBFE是矩形
∵四边形ABCD是平行四边形,
∴OB=OD
∵E为AB中点,
∴AE=BE
∴OE为△ABD的中位线,
∴OE∥AD,
∴∠BOE=∠BDA,
∵AD⊥BD,
∴∠BOE=BDA=90°,
∵四边形OBFE是平行四边形,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.

理由:∵OE为△ABD的中位线,
∴OE=
| 1 |
| 2 |
∵O为BD中点,
∴OB=
| 1 |
| 2 |
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
| 1 |
| 2 |
∵O为BD中点,
∴OB=
| 1 |
| 2 |
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
| 1 |
| 2 |
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
看了 如图,在▱ABCD中,对角线...的网友还看了以下:
分解因式a(a-b-c)+b(c-a+b)+c(b-a+c)的结果是()A.(b+c-a)2B.( 2020-04-08 …
matlab解中学三角函数方程数学题,不会求大大~~~~~~~~~~[a,b,c,A,B,C]=s 2020-05-14 …
一道解析几何的题,急.如图在直角坐标系xoy中,P(1,1/2)到抛物线C:y²=2px(p>0) 2020-06-14 …
为了应用平方差公式计算(a-b+c)(a+b-c),必须先适当变形,下列各变形中,正确的是()A. 2020-07-31 …
用公式法化简逻辑函数F=AB+A'C+B'CF=AB+A'C+B'C=AB+A'C(B+B’)+B 2020-08-01 …
为了应用平方差公式计算(a-b+c)(a+b-c)必须先适当变形,下列变形中,正确的是[]A.[( 2020-08-02 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
三条不同直线的a,b,c,其中正确的命题个数是()(1)若a∥b,b∥c,则a∥c;(2)若a⊥b 2020-08-02 …
已知a、b、c满足a<b<c,ab+bc+ac=0,abc=1,则()A.|a+b|>|c|B.|a 2020-11-01 …
下列能保证a⊥∂(a,b,c为直线,∂为平面)的条件是()A.b,c⊂∂.a⊥b,a⊥cB.b,c⊂ 2020-11-02 …